Magic squares have fascinated mathematicians for centuries. Today, they continue to do so as part of our Ri Masterclasses for young students around the UK, as they explore the wonders of mathematics, geometry and computer science. Magic squares are rich in history, appear in some surprising places, and have astonishing patterns within them.
Alison Eves, our Primary Mathematics Masterclasses Coordinator, tells us some of her favourite facts about these wondrous shapes.
Over to you, Alison…
What’s a magic square?
If you lay an array of numbers in a grid, and the sums of the numbers in each row, each column, and both main diagonals are the same…congratulations! You’ve got yourself a magic square.
Magic Squares: then and now
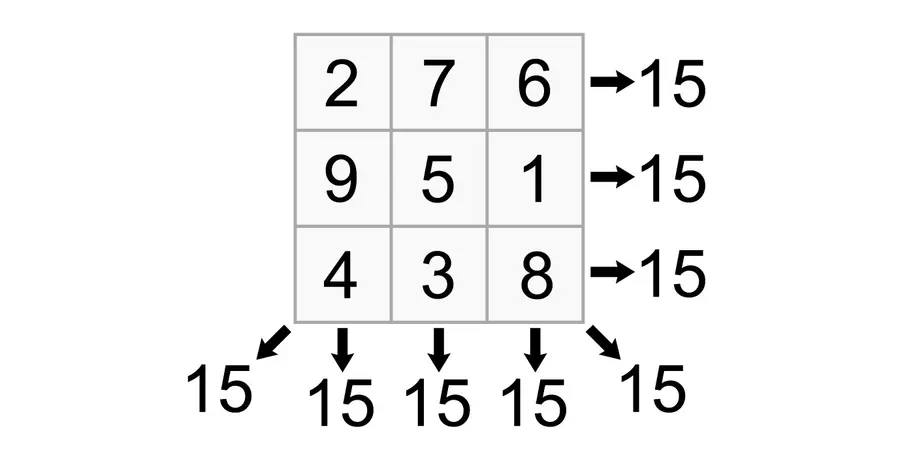
The first recorded magic square is the Lo Shu Square, found in ancient China about 5000 years ago. Legend has it that when the Lo River was in flood, the people became increasingly desperate, and they asked the river gods to save them. In response a mystical turtle emerged to rescue them from the deluge, with a pattern inscribed on its back. The pattern was a 3x3 grid of nine squares, each containing one of the numbers between 1 and 9. No matter which way the 3 numbers in each row, each column and both diagonals of the square were added, the sum was always 15. This arrangement is what we now know as the 3x3 magic square. (This particular version is known as a Normal Magic Square, where the grid is n x n and contains each of the integers 1-n2).
I really enjoy that people separated from me in time and space by thousands of years and thousands of miles enjoyed the same mathematical patterns as I do today. This constant, unchanging nature is one of the most satisfying aspects of mathematics for me-once something is proved true, it is eternally true.
Magic Squares – simple and complex
There is essentially only one way of arranging the integers 1–9 in a 3x3 magic square: in the Ri Masterclass I ask the 10-year-old students to find different arrangements, and then we discuss whether we think we have one solution, or eight. This is the simplest possible magic square, of order 3.
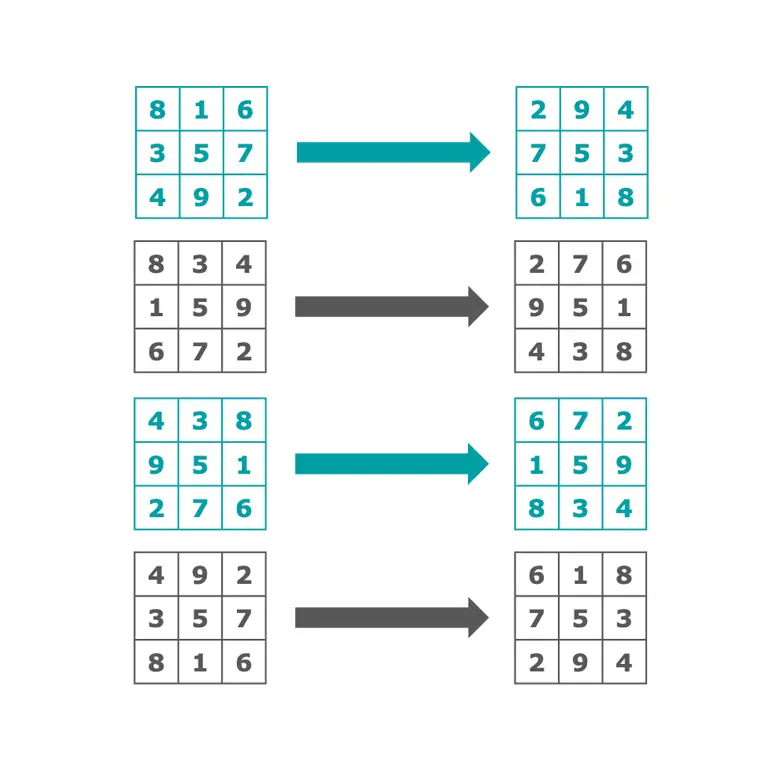
Go up one degree of complexity, and what happens? Something very surprising!
It is known that there are 880 distinct solutions for a 4x4, or order 4 magic square, containing the numbers 1-16, magic total 34. Another wonderful attribute of mathematics – the answers often surprise you, defying your first instinct.
Go up again to a 5x5 magic square (numbers 1–25 and magic total 65) and research has proved there are no less than 275,305,224 different solutions.
Now I know that you are asking what any self-respecting mathematician (=person) would want to know: how many solutions for a 6x6 magic square (numbers 1-36 and magic total 111)? The incredible fact is (although I do actually believe it) that is an unsolved problem. It is a subject of ongoing mathematical research. Statistical techniques indicate that there are probably of the order of 17,700,000,000,000,000,000 individual solutions.
It both blows my mind and delights me that a problem that I can investigate in full in an Ri Masterclass (how many magic squares of order 3 are there?) can in 3 straightforward steps become something so complex that no one (yet) knows how many answers there are.
Magic Squares – art and history
The first occurrence in Western art of a magic square is in an etching by Albrecht Dürer, entitled Melencolia I. Dürer was fascinated by both art and mathematics, and combines the two interests in this picture. The magic square is of order 4 and is in fact a Pan diagonal Magic Square (also known as a panmagic or perfect) magic square, i.e., one in which the entries of the broken diagonals also sum to the magic constant of 34.
In fact, there are many other patterns of four digits within the Dürer square which add to 34: perhaps you’d like to search for some yourself (pattern spotting is one of my favourite descriptions of what “doing mathematics” often entails.)

When on holiday in Barcelona I was delighted to spot another magic square, chiselled into the facade of the Sagrada Familia. You will see that this is not a normal magic square, as it has repeated integers, and the magic total is 33. It is in fact being used to tell the story of Jesus’ life, depicted in stone on the cathedral. It is carved into the stone alongside the figures showing the final scenes of Christ’s life, when he was aged 33.

On closer examination I noticed an amazing connection between the Dürer and the Sagrada Familia magic squares. Remember that there are 880 different 4x4 normal magic squares? It (literally) turns(!) out that the Sagrada Familia square and Dürer’s magic square are essentially the same solution, just turned through 180° and with 4 of the numbers reduced by 1, in order to produce a magic total of 33 instead of 34.

This is a real “Wow!” moment in the Magic square Ri Masterclass.
I could go on waxing lyrical about the joys of Magic Squares, but I am running out of space here. I will however be sharing further insights and activities based on magic squares at a holiday workshop in July. There is so much more to enjoy and discover together: do join me at the Ri holiday workshop or post responses below
Over 40 years of making maths fun
Ri Masterclasses are a series of workshops where students can explore mathematics and computer science outside the confines of the classroom, through hands-on extra-curricular workshops, and students get to attend a Ri Masterclass series by being nominated by their teacher.
We wanted to share our love for mathematics further, so we picked some of the most popular Masterclass topics and turned them into one-day Holiday Workshops for children ages 7+.
